In 1973, UC Berkeley was sued for discrimination against women in graduate school admissions. The data of percent acceptance indisputably show that, if a male applies to Berkeley, he is more likely to be admitted than a female that applies (44% vs. 35%).
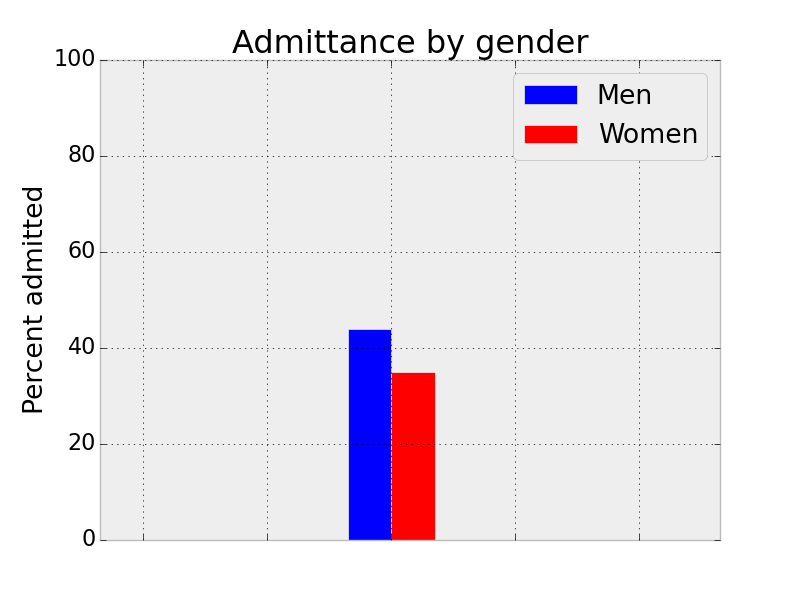
On the basis of this data, one may propose the causal conclusion that Berkeley is biased against females. However, this is just an example of Simpson’s Paradox, a non-intuitive phenomena where a correlation that is present in several groups is the opposite of what is found when the groups are amalgamated together. In this example, a group refers to a department at the university.
If we partition the data by department, we reveal that, in 4/6 of the departments, a female applicant is more likely to be accepted than a male applicant– the opposite conclusion of Berkeley being biased against females! This is the paradox in Simpson’s paradox: in the aggregate data, Berkeley appears biased against female applicants; when the data is partitioned by department, it does not. In the remaining two departments, the disparity between men and women is not as drastic as the amalgamated data above.
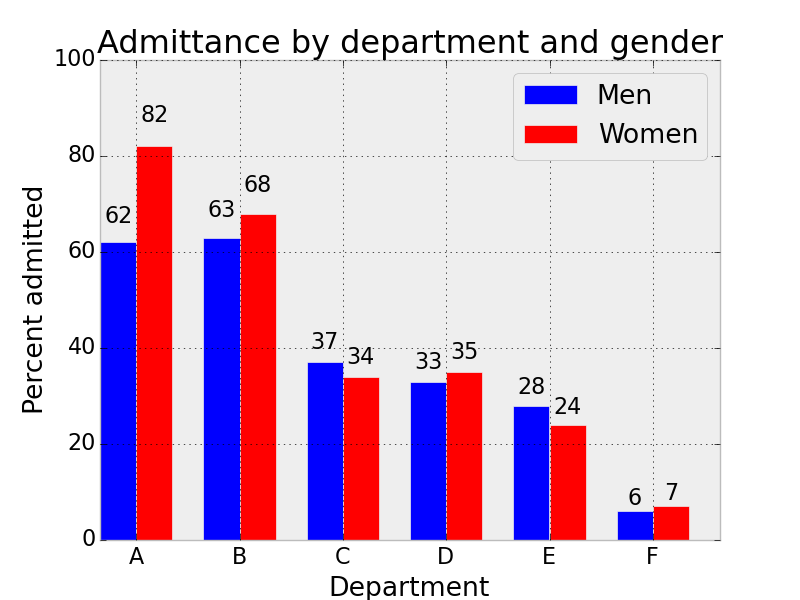
The reason that Berkeley appears biased against female applicants in the aggregated data set is because of a lurking variable that had not been considered when the law suit was filed, namely the distribution of the applications of males and females to the different departments. Let us look at the number of males and females that apply to each particular department. We see that the least competitive departments A and B are heavily dominated by male applicants, while the most competitive departments E and F are dominated by female applicants.
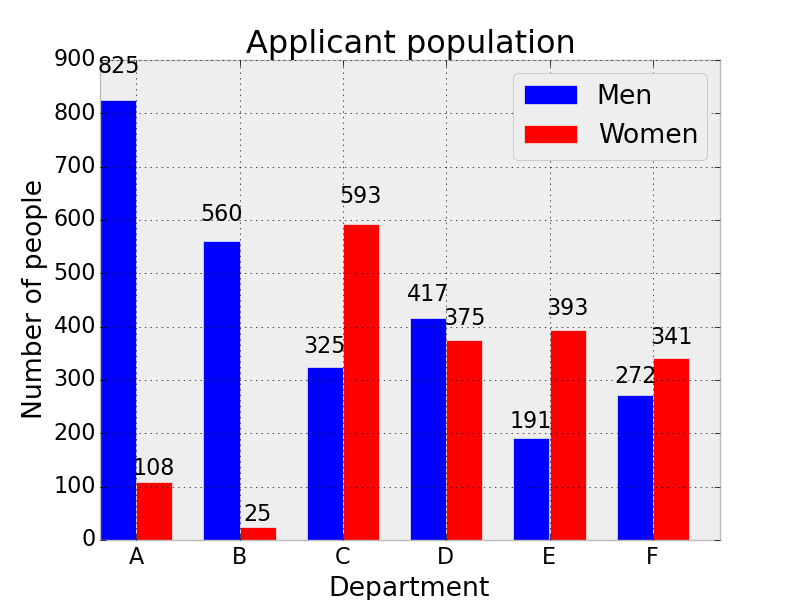
The reason that a significantly higher percentage of male applicants are accepted than women in the aggregated data is that females applied to more competitive departments than the males did. Thus, as a whole, it was more likely that a male applicant would be accepted to Berkeley. But, this is because, according to the data, a female was more likely to apply to a department that has a lower average acceptance rate.
The Simpson’s Paradox elucidates the need to be skeptical of reported statistics that may be drastically dependent upon how the data is aggregated [1] and to be aware of lurking variables that may negate a conclusion about what _causes _the correlations observed in data. Several other examples, such as batting averages, kidney stone treatments, and birth weights, of a real-life Simpson’s paradox can be found on the Wikipedia page [2] where this data was taken from.
[1] P. J. Bickel, E. A. Hammel, J. W. O’Connell. Sex Bias in Graduate Admissions: Data from Berkeley. Science 187, (4175). 1975. pp. 398-404.
[2] http://en.wikipedia.org/wiki/Simpson’s_paradox
comments powered by Disqus