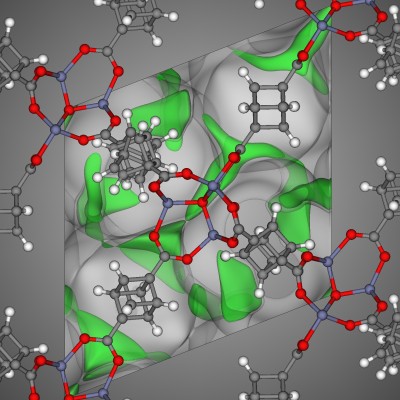
The unit cell of many crystals, for example a metal-organic framework, can be described by three basis vectors $a_1$, $a_2$, and $a_3$ that form a three-dimensional parallelpiped. One can conveniently express any point $x$ inside the unit cell of the crystal as a linear combination of these vectors:

$x = f_1 a_1 + f_2 a_2 + f_3 a_3$,

where $f_i \in [0, 1]$ are fractional coordinates. For example, in two dimensions, the shaded gray area formed by the parallelogram of the two vectors $a_1$ and $a_2$ in Fig. 1 could describe a unit cell of a crystal.

The point $x$ in Fig. 1 can be described as $\frac{1}{2}a_1+ \frac{1}{2}a_2$.

To mimick an infinite crystal during molecular simulations, we can consider only the home unit cell and impose periodic boundary conditions. For example, the electrostatic potential $\phi(x)$ inside the pores of a metal-organic framework is a periodic function since we model the crystal as infinitely repeating. Using the basis vectors $a_1$, $a_2$, and $a_3$, we can express the periodicity of $\phi(x)$ as:

$$\phi(x + n_1 a_1 + n_2 a_2 + n_3 a_3) = \phi(x),$$

where $n_i\in \mathbb{Z}$, that is $n_i$ are integers. Fig. 2 shows a point $x$ in the home unit cell formed by $a_1$ and $a_2$ and its periodic images $x+n_1 a_1 + n_2 a_2$ for our two-dimensional example (here we show $n_1\in\{-1,0,1\}$ and $n_2\in\{-1,0,1\}$).

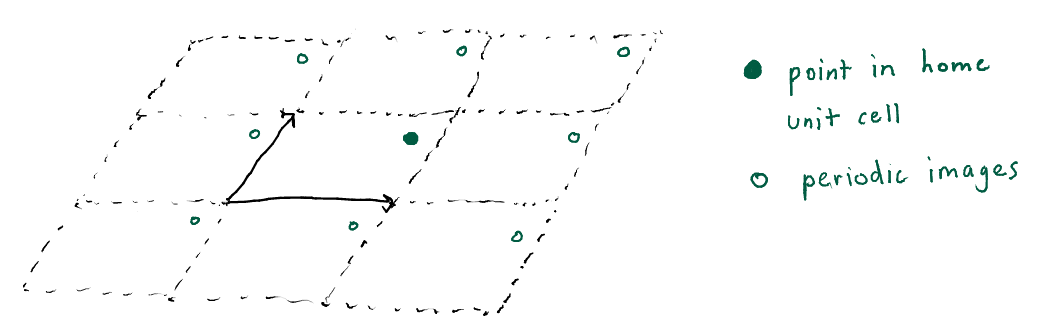
The points $n_1a_1 +n_2a_2+n_3a_3$ for $n_i \in \mathbb{Z}$ that form the corners of the unit cells are called a Bravais lattice.

As the electrostatic potential $\phi(x)$ has the same periodicity as the Bravais lattice describing the unit cell, we can expand it in a discrete Fourier series:

$$\phi(x)=\phi(f_1, f_2, f_3) = \displaystyle \sum_{n_1=-\infty}^{\infty} \displaystyle \sum_{n_2=-\infty}^{\infty} \displaystyle \sum_{n_3=-\infty}^{\infty}c(n_1, n_2, n_3) e^{2\pi i (n_1 f_1 + n_2 f_2 + n_3 f_3)},$$

essentially viewing $\phi(x)$ as a function of fractional coordinates $(f_1, f_2, f_3)$, which each have a periodicity of 1.0. The Fourier coefficients are denoted as $c(n_1, n_2, n_3)$.

We can instead express the above Fourier series as a sum over vectors $k$:

$$\phi(x)= \displaystyle \sum_{k} c(k) e^{i k \cdot x},$$

where vectors $k$ are in the set:

$$k = n_1 b_1 + n_2 b_2 + n_3 b_3.$$

The vectors $b_i$ are reciprocal lattice vectors, defined as:

$$b_i \cdot a_j = 2 \pi \delta_{ij}.$$

This way,

$$k \cdot x = (n_1 b_1 + n_2 b_2 + n_3 b_3) \cdot (f_1 a_1 + f_2 a_2 + f_3 a_3) = 2 \pi (n_1 f_1 + n_2 f_2 + n_3 f_3),$$

as in the first time we wrote the Fourier series expansion of $\phi(x)$.

We can obtain the reciprocal lattice vectors from a given Bravais lattice by solving the matrix equation $[a_1 a_2 a_3]^T [b_1 b_2 b_3] = 2\pi I$.

In conclusion, functions that have the same periodicity as the Bravais lattice can be expressed as a Fourier series over the reciprocal lattice vectors.

comments powered by Disqus